サイクロイド振り子の等時性
単振り子では、周期が振幅に依存する。 ところが、このサイクロイド振り子は振幅に寄らず周期が一定になるという性質を持つ。 上のアプレットでは振幅を変化させることができる。色々な振幅で周期を確認してみてほしい。
サイクロイド振り子は、半径 r の円によってつくられるサイクロイド二つの間に挟まれた振り子である。 紐(ひも)の長さが 4r であるときには、振り子の小球自身が描く軌跡もサイクロイドとなる(青線)。
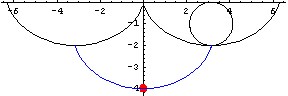
ところで、サイクロイドとは何かというと円上のある一点に注目して、円を滑ることなく転がしたときにその点が描く軌跡である。

さて、何故サイクロイド振り子では周期が一定になるのだろうか。 単振り子では、振幅が大きいとき周期が振幅に依存してしまう。(→単振り子) 単振り子の周期は振幅だけでなく、糸の長さにも依存する。 糸の長さが長いほど、周期は大きくなる。 つまり、振幅が大きくなると周期も大きくなるが、糸が短くなると周期は小さくなるのである。
さて、上のサイクロイド振り子の振れる様子をよく見てみると、大きく振れているときにはサイクロイドの壁面に糸が張り付いて有効な糸の長さが短くなっているのがわかる。
振幅による周期の増加分と糸を短くすることによる減少分がうまく相殺して周期一定となるような振り子がこのサイクロイド振り子でなのである。
そういったわけで昔はよく見かけられた、振り子時計に使われていた振り子は、実は単振り子ではなくサイクロイド振り子だろうと思う。
(次ページへ続く)