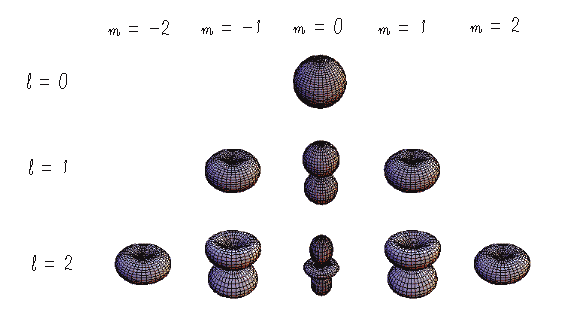球面調和関数

 極座標でのシュレディンガー方程式で見たように、ポテンシャルが球対称であるときには動径部分と角部分に方程式を分離することができた。 角部分の方程式は、

であった。λ は分離定数である。

 この方程式はさらに、Y(θ,φ) = Θ(θ)Φ(φ) として、分離定数を ν とすれば


と分離できる。

 このうち、φ に関する方程式は簡単に解くことができる。境界条件を考慮すると ν がある整数の二乗になっていることが必要 になる。 最終的に解は次のように書ける。

これで、φ に関する方程式は解けた。

 さて、θ に関する方程式であるが ν=m² であることに注意して、w = cosθ (-1≤w≤1) と変数変換を行う。


 m = 0 のときに物理的に許された解は、Legendreの多項式 P_l と呼ばれる。母関数から、Legendreの多項式の性質を調べると λ= l(l+1) がわかる。
 m ≠ 0 でも、λ=l(l+1), |m| < l ならば物理的に許される解を持つ。
この解は Legendreの陪関数 (associated Legendre function) と呼ばれていて Legendreの多項式を使って次のように表すことができる。

 Legendreの陪関数に対する規格化定数 N_lm を使えば、完全な波動関数の角部分 Y_lm(θφ) は次のように書ける。

この関数は球面調和関数と呼ばれている。( |m| < l , l = 0, 1, 2, ...)

 これは、三次元極座標表現に置けるシュレディンガー方程式の角部分の方程式の解であるがポテンシャル V(r) の形には依らないことに注意。

球面調和関数 Y_lm(θ,φ) の大きさの角度依存性をプロットすると次のようになる。