
とかける。もしポテンシャルが球対象である(V(r)=V(r))ならば、球座標系で書くと次のようになる。

この方程式は、r を含む部分と θ, φ を含む部分とに分けることができる。
u(r,θ,φ) = R(r) Y(θ,φ) とすると次のようになる。λ は分離定数である。
(動径部分) :

(角部分) :
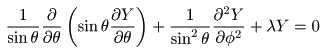
そして、角部分はさらに θ を含む部分と φ を含む部分に分離することができる。
Y(θ,φ) = Φ(φ) Θ(θ) として、分離定数を ν とすれば次のようになる。


こうして、極座標でのシュレディンガー方程式はポテンシャルが球対象である(θ,φに依らない)ならば、それぞれの座標成分ごとに分離することができる。 そして、角部分の方程式 Y(θ,φ) = Θ(θ) Φ(φ) はポテンシャル V(r) の形に依らないことがわかる。