Taylor展開とは、任意の関数が

というように展開できるというものである。(詳細[pdf 36kB])
たとえば、 y = sin(x) を taylor展開すると

となる。
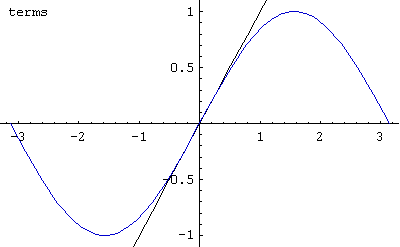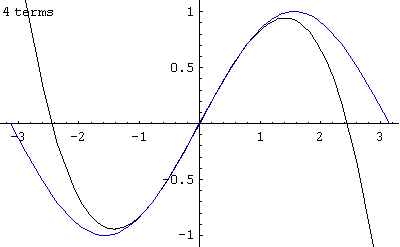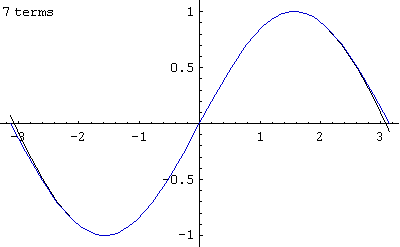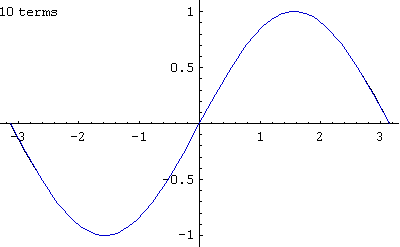
この式の n = 1 からの収束の様子を -π から π の範囲でアニメーションさせたのが上の画像である。
n = 4 くらいまで足すと、すでにほぼ収束してしまっている。(画像中の数字の1/2の数が上式での n にあたる)
しかしここで、
「なんて、収束性のいい展開式なんだ。」
と、感心してはいけないようである。

今度は -2π から 2π までのアニメーションである。 確かに、n = 4 までで、-π から π までの収束は十分であるように思えるが、そのあとは駄目駄目である。 なので、そのあとも足し続けてみた。すると n = 8,9 くらいで、この範囲では収束をしているように見える。 しかし、それはやっぱりこの範囲までであろう。 広い範囲での収束を期待するならばその分だけ項数を増やさねばならないだろう。 もちろん、ある点のまわりの値だけが欲しいならばその点のまわりで展開すれば良く、項数がそんなに必要になるわけではない。
Fourier級数の収束の仕方と比べてみると面白いだろう。