そのうちこのサイトにも説明を載せる予定。
このページは物理学実験 2 の p53 「偏光」 が全然わからなかったのでなんとなく作ってみた。
結晶二軸(直交)を軸とする。

------- 緑色線 : 入射光
------- 赤色線 : 異方性結晶通過光
------- 水色線 : 検光子通過光
略解説
・電場ベクトル上記のアプレットでは、電場ベクトルを次の式により決定している。・マリュスの法則
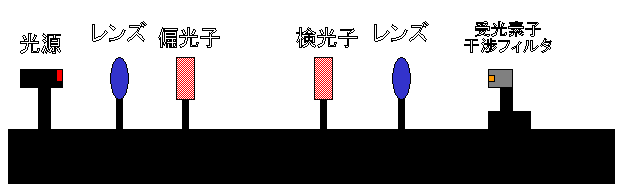
以下のような構成の実験装置で実験を行う。
光源から出た光は偏光子によって、直線偏光となる。
偏光子と検光子の間には異方性を持つ物質を挟んでいないので φ = 0とする。
このとき、入射光 Ei と透過光 Et の間には次の関係が成り立つ。θ と ζ の角度差を 90度にすると、Et = 0 となることから確認できる。
・異方性物質
以下のような構成の実験装置で実験を行う。
直行ポラロイドの間に透明な物質を種々挿入し、この光学系に光を入射したとき何の変化も観察されない場合と、 透過光に変化が現れる場合がある。前者の挿入物質を光学的に等方な物質、後者を異方性を持つ物質と呼ぶ。 異方性物質が示す性質を複屈折 (double refraction) と呼ぶ。異方性物質は直交する光学軸を有し(一般には斜交している)、 その軸方向によって屈折率が異なっている。この 2軸を f軸および s軸と呼ぶ。f軸方向の偏光成分に対する屈折率は s軸方向の 偏光成分に対するそれより小さい (nf < ns)。すなわち前者の透過速度が大きい。
f軸方向と s軸方向の直線偏光波が同位相で、一定の厚さの複屈折物質に入射した場合、透過後の両成分の位相には一定の位相差(φ)が生じる。
f軸方向とs軸方向の光波に生じる位相差 φ は、
である。ここに、 d は複屈折物質の厚さ、λ は光の波長。この位相差のため、複屈折物質を透過した光波は一般に楕円偏光状態にある。特に、 φ = 0, π/2, および π ではそれぞれ傾き + 1 の直線、 円、および傾き -1の直線となる。
φ = π/2, πのとき、その位相差は波長にしてそれぞれ λ/4, λ/2 であるからこのような複屈折物質を 1/4波長板、1/2波長板と呼ぶ。
・装置写真
装置写真が見てみたいとの要望がありましたので掲載します。 光学系の調整は行ってない状態です。